Main Menu Works

Cool Math Question

This is from the SAT. It gave me a bit of a pause but was fun to work through.

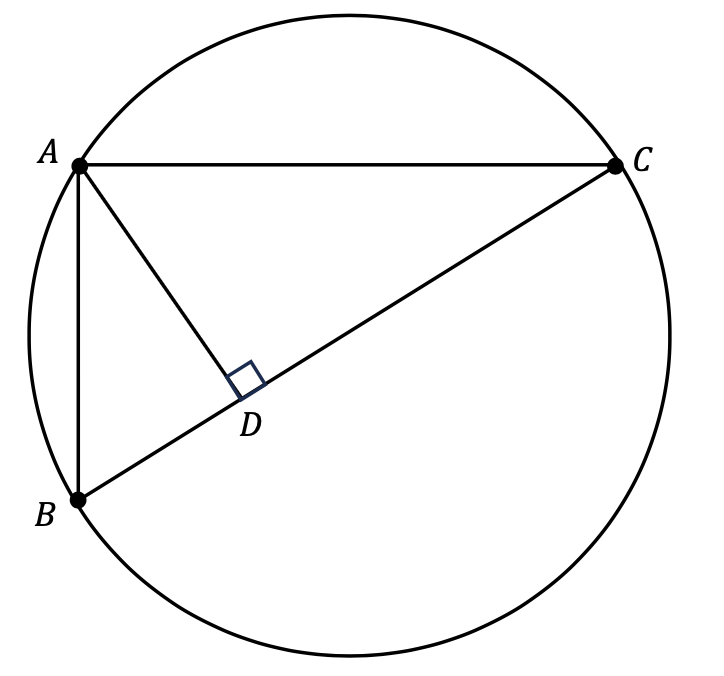
The first thing to realize is that \(\triangle ACB\) is a right angle. If you have two chords intersecting at a point that lies on the circumference of a circle, they meet at right angles.

The second thing to realize is that if we can figure out the length of the line \(AD\), we can use Pythagoras' to figure out the length of \(BD\).

We can figure out the length of \(AD\) if we can get \(\angle ABC\). We'll use the sine of that angle.

And, finally, we can get \(\angle ABC\) through some regular ol' trigonometry. We know two sides of this right angle triangle (\(\triangle ABC\)). For this, we'll get \(\angle ACB\), which turns out to be \(\arcsin(\frac{\sqrt{363}}{132})\) . Now, we'll subtract that value from 90 to get \(\angle ABC\). We'll keep this value exact; it's \(90 - \arcsin(\frac{\sqrt{363}}{132})\).

We'll plonk this angle into an equation with sine. \(\sin(90 - \arcsin(\frac{\sqrt{363}}{132})) = \frac{AD}{\sqrt{363}}\). Solve for AD and you get around about 18.85, but we won't round off. We'll call this value "A".

Now, we'll use Pythagoras' to solve for BD. \(\sqrt{(\sqrt{363})^2 - A^2}\) comes to exactly \(\frac{11}{4}\). This is the length of BD.

Hence, \(\frac{BC}{BD}\) comes to \(\frac{132}{\frac{11}{4}}\) which simplifies to 48 exactly. Wow!

There are probably simpler approaches, but this worked for me!

This article was written on 28/06/2024. If you have any thoughts, feel free to send me an email with them. Have a nice day!